Neuronale Netzwerke als numerische Methode

2024-09-08
Das Wort KI ist omnipresent, seit die Text- und Bildgeneratoren von ChatGPT und Konsorten sich auf dem Terrain der natürlichen Sprachen bewegen, das sonst uns Menschen vorbehalten war. Zum Teil ist es Hype: Das Modewort ersetzt NFT, das seinerseits Blockchain ersetzte und jede Büroanwendung verkauft seine Technologie mit KIplus. Zum Teil ist des disruptiv und ersetzt bisherige Prozesse, setzt uns aber neuen Abhängigkeiten aus.
Neuronale Netze als Teil der KI sind aber in erster Linie durchaus nützliche numerische Methoden, die zur Lösung von wissenschaftlichen und technischen Problemen eingesetzt werden können, für die es keine analytische Lösung gibt oder deren Lösung sehr komplex ist.
Die meisten erinnern sich aus der Schulzeit and die Bücher mit den Physikformeln, die alle Gesetze aufzählen, welche die Welt zusammenhalten. Newton hat es im 17. Jahrhundert geschafft, die damals beobachtbaren physikalischen Phänomene der Mechanik mit wenigen mathematischen Formeln zuverlässig zu beschreiben. In der Physik gilt ja bekanntlich der Tatbeweis. Ob eine Formel richtig oder falsch ist, kann nicht logisch bewiesen werden. Es ist entscheidend, ob die Formeln die Daten der physikalischen Experimente getreu abbilden.
Es gibt aber nicht für alle Phänomene eine passende Formel. Ein populäres Beispiel ist das Dreikörperproblem. Körperprobleme beschreiben die physikalische Wechselwirkung zweier Körper im Raum. Dazu gehören Impulse, wenn die Köper zusammentreffen, wie auch die Gravitation, wenn die Körper umeinander kreisen. Das Zweikörperproblem hat Kepler analytisch mit einem Gleichungssystem gelöst. Doch schon für das Dreikörperproblem gibt es keine analytische Lösung. Lui Cixin beschreibt im gleichnamigen Roman ein Sonnensystem mit drei gleich grossen Sternen. In dieser Konstellation ist die Bewegung chaotisch.

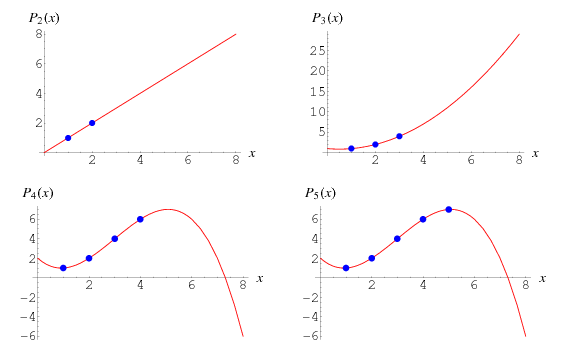
Newton hat aber nicht nur analytische Formeln für die klassische Mechanik hergeleitet, sondern auch selber numerische Methoden entwickelt, nämlich die Newtonsche Interpolation. Wenn für eine Funktion gewisse Punkte bekannt sind, kann man mit der Interpolation eine polynominale Kurve definieren, die durch diese Punkte geht. Dabei benutzt er eine rekursive Methode, welche die Differenzen sukzessive dividiert. Die Gleichung, die er damit erhält, ist nicht physikalisch wahrer oder falscher als eine analytische Herleitung. Solange sie mit Messdaten vereinbar ist, ist sie physikalisch gültig, zumindest für den Bereich innerhalb der extremen Messdaten. Wenn wir den Bereich der Messdaten verlassen, handelt es sich um Extrapolation.
Ein Jahrhundert später entwickelte de Buffon die Monte Carlo Methode, um die Zahl Pi numerisch zu berechnen. Er warf eine grosse Anzahl relativ kleiner Nadeln zufällig auf eine Fläche und zählte aus, wieviele Nadeln sich innerhalb und wieviele sich ausserhalb eines Kreises befanden. In den 1930er Jahren machte Fermi Monte Carlo Simulationen mit elektronischen Rechenmaschinen, die Zufallszahlen erzeugen konnten. Im Manhattan-Projekt wurden diese Simulationen benutzt, um die Atombombe zu entwickeln.
Neurale Netze sind mit Interpolation und der Monte Carlo Methode vergleichbar, als sie auf Messdaten berufen und daraus Gesetzesmässigkeiten ableiten. Die neutralen Netzdaten sind jedoch viel allgemeinerer Natur, weil sie durch die mehrschichtige Kombination von Schwellwerten und Verstärkern komplexe nonlineare Beziehungen abbilden können.
Sie eignen sich deshalb zur Lösung von Optimierungsproblemen, die klassisch einen sehr hohen Rechenaufwand benötigen. Beispiele wären die Berechnung des kürzesten Wegs durch ein Netzwerk, der Ausgleich zwischen Stromproduktion und Stromverbrauch wie auch die Analyse und die Produktion von natürlicher Sprache.
Zu bedenken ist jedoch, dass diese Systeme immer nur innerhalb der Messdaten gültige Resultate liefern. In diesem Bereich können wir sie akzeptieren, auch wenn wir sie nicht nachvollziehen können. Ausserhalb der Messdaten sind sie jedoch genauso problematisch, wie wenn man die Interpolation zur Extrapolation verwenden würde.
Vollautomatisierte Systeme sind deshalb problematisch, wenn ihnen keine Grenzen gesetzt werden. Es kann nicht sein, dass ein Stromnetzwerk selber entscheidet, ein ganzes Quartier abzuschalten. Wenn neuronale Netzwerke eingesetzt werden, muss man immer die Berechtigungen und Extremsituationen mitdenken. Im Idealfall würde das System der neuroyalen Netze selber zum Schluss kommen, dass es mir den Eingabedaten überfordert ist und selber keine sinnvollen Ausgabedaten produzieren kann.
Siehe auch:
LLMs don’t do formal reasoning - and that is a HUGE problem
The inability of standard neural network architectures to reliably extrapolate — and reason formally — has been the central theme of my own work back to 1998 and 2001, and has been a theme in all of my challenges to deep learning, going back to 2012, and LLMs in 2019.
I strongly believe the current results are robust. After a quarter century of “real soon now” promissory notes I would want a lot more than hand-waving to be convinced than at an LLM-compatible solution is in reach.
What I argued in 2001, in The Algebraic Mind, still holds: symbol manipulation, in which some knowledge is represented truly abstractly in terms of variables and operations over those variables, much as we see in algebra and traditional computer programming, must be part of the mix. Neurosymbolic AI — combining such machinery with neural networks – is likely a necessary condition for going forward.
Gray Marcus
https://garymarcus.substack.com/p/llms-dont-do-formal-reasoning-and
und ein Paper von Apple
GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models
Our findings reveal that LLMs exhibit noticeable variance when responding to different instantiations of the same question. Specifically, the performance of all models declines when only the numerical values in the question are altered in the GSM-Symbolic benchmark. Furthermore, we investigate the fragility of mathematical reasoning in these models and demonstrate that their performance significantly deteriorates as the number of clauses in a question increases. We hypothesize that this decline is due to the fact that current LLMs are not capable of genuine logical reasoning; instead, they attempt to replicate the reasoning steps observed in their training data.
